P ↔ (p ∧ q) ∨ (p ∧ ¬q) Y que resulta en esta Tabla de Verdad El procedimiento consiste en ir solucionando los valores de los conectores para cada interpretación de las variables Aunque no aparezcan los paréntesis, estos son necesarios para resolver los conectores de forma ordenada, desde los paréntesis más interiores hasta el Encuentra una respuesta a tu pregunta Realizar las siguientes tablas de verdad 1 (∼ p ∨ r) ∨ q 2 (p ∨ q) ↔ (∼ p ∧∼ q) 3 (r ∨ q) ↔ r 4 (p ∧ q) ↔ (∼ q →∼ r)Absorción (lógica) Absorption (logic) La absorción es una forma de argumento válida y una regla de inferencia de la lógica proposicional La regla establece que si implica , entonces implica y La regla permite introducir conjunciones a las pruebas Se llama ley de absorción porque el término es "absorbido" por el término en el
Tabla De Verdad De La Bicondicional
P q p q tabla de verdad
P q p q tabla de verdad-5 13 Construye las tablas de verdad e indica si se trata de tautologías, contradicciones o indeterminaciones (contingencia) a ¬p v q b (p ^ q) → p c p ↔ ¬p dElabora La Tabla De Verdad De Los Siguientes Razonamientos ¬ (P→Q) ∨ (¬P∧¬Q) (P→Q∧¬Q) →¬P 121 usuarios buscaron estas tareas del colegio para responder el mes pasado y 98 lo están haciendo ahora mismo, vamos a hacer tus tareas y deberes rápido Esta Tarea Respondida es nivel Secundaria y pertenece a la categoría Filosofía




Tautologia Contradiccion Contingencia Ejercicios Resueltos De Implicacion Y Equivalencia Logica Pdf
Es incorrecto puesto que podría ser mayor de edad y no tener permiso de conducir, de ahí la importancia de no confundir la implicación (si p, entonces q) con el bicondicional (p si y solo si q), es decir, p es condición para que se pueda dar q, pero p no implica necesariamente q (ser mayor de edad es condición necesaria, pero no suficienteFormulario Angelica Ayora 1 Tablas de verdad 11 Conjunción, ∧ Se lo lee "y", si el valor de verdad de una de las proposiciones simples es falso, entonces todo es falso P Q P ∧Q V V V V F F F V F F F F 12 Disyunción, ∨ Se lo lee "o", si el valor de verdad de una de las proposiciones simples es verdadero, entonces todo esDe este modo, la tabla de valores de verdad de p ⇔ q puede obtenerse mediante la tabla de (p ⇒ q) ∧ (q ⇒ p), como Ejemplo Sea i) a = b si y sólo si a² = b² El enunciado está compuesto por las proposiciones p a = b q a² = b² Esta doble implicación es falsa si p es F y q es V En los
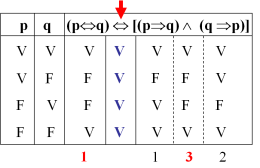
Para construir tablas de verdad solo debes realizar unos pasos muy sencillos y claros A continuación pasaremos a explicar cada uno de los pasos necesarios para hacer una tabla de verdad, utilizando como ejemplo la sentencia (p→q)^r Determina el número de filas de la tabla de verdadEjercicios 1Se define el operador lógico % con la siguiente tabla de verdad P% P Q Q V V F V F V F V F F F V Desarrolle el siguiente esquema molecular y dé como respuesta la cantidad de proposiciones verdaderas de su matriz principal ∨ ( p → q ) ( q ∨ p) ↔ p a) 2 b) 3 c) 0 d) 1 2Es verdadera, por tanto concluimos que P ⇒ Q, es decir, p ∧(p → q) ⇒ q Otra forma de determinar si P ⇒ Q es verificar si P→ Q es una tautología Veamos como hacemos esta otra forma de comprobación por medio de una tabla de verdad p q p → q p ∧(p → q) p ∧(p → q) →q VV V V V V F F F V F V V F V F F V F V
4D (¬p →→→→q) ∧∧∧∧ (p →→→¬q) 5 Ojos que no ven, corazón que no siente 1E (p ∧∧∧q) →→ → ¬r 9 Formaliza las siguientes proposiciones "Si tuvieran que justificarse ciertos hechos por su enorme tradición entonces, si estos hechos son inofensivos y respetan a todo ser viviente y al medio ambiente, noUna tabla de verdad, o tabla de valores de verdades, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar 1 Fue desarrollada por Charles Sanders Peirce por los años 10, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logicophilosophicus, publicado en 1921Con Tablas de la Verdad se analiza una Proposición Lógica para saber si es una tautologia o contradicción o contingencia Más videos sobre LÓGICA https//w




Tablas De Verdad Negacion Conjuncion Disyuncion Youtube




Ejercicios De Logica Solucionario Proposicion Verdad Logica
1 Qué tipo de proposición se obtiene al construirla tabla de verdad de (p∧~q)↔(p→q)?Contradicción 2 Construya la tabla de verdad de (~p∨q)∧~qDar como respuesta los valores del conector principal FFFV 3 Elabore la tabla de verdad de (p→q)∨(~p∧q)y encuentre la proposición más simple equivalente a ella p q 4 Hallar los valores del conector principal de la tabla de verdad de (p∨q)∧(p∨~qEs un trabajo más laborioso que difícil , Tengo conocimientos acerca de ese tema Ejercicio proposición n° 2 con tabla de verdad 2 Si el Rh de la futura madre es negativo debe analizarse inmediatamente después de cada parto la sangre del recién nacido, si ésta es Rh positivo ha de administrarse a la parturienta el suero apropiado si se desea evitar complicaciones en otros hijos p el Rh de la futura madre es negativo q el Rh de la futura madre



Tautologia Ecured




Tablas De Verdad Problemas Resueltos De Logica Matematica Proposicional Pdf
View unemi1docx from ESTADISTIC 101 at Escuela Politécnica del Ejercito 3 Dadas las siguientes proposiciones Indicar cuál (o cuáles) es una Contingencia utilizando tablas de verdad 1) (p ∧Ejercicios de tablas de verdad tabla de verdad proposiciones las tablas de verdad son, por una parte, uno de los métodos más sencillos conocidos de la lógica Construir la tabla de verdad de a (p∧~q)∨q∧~p b (p∧q)∧p→(p∨q) 1 Ver respuesta nicolasangamarca721 está esperando tu ayuda Añade tu respuesta y gana puntos waldolandaricaldi waldolandaricaldi Explicación paso a paso PARA CONSTRUIR LA TABLA TIENES QUE UBICAR EN ORDEN




Capitulo I Logica Y Conjuntos Ppt Descargar




Practica 2 Dplm Contradiccion Proposicion
PROPÓSITO • Para saber siView Tabla de verdadxlsx from MATH 2 at Loyola Marymount University P V V F F MAESTRA NATHALIE BRITO ALUMNA SUSANY FELIZ MEDINA 1 p∧q Método alternativo de construir una tabla de verdad p q ¬ (p ∧ ¬ q) 1 1 1 0 0 1 0 0 42 51 Evaluación Continua 1 Construya las tablas de verdad de las siguientes proposiciones 1 p ∨ ¬p 2 p ∧ ¬p 3 ¬ (p ∨ q) 4 ¬p ∧ ¬q 5 ¬ (p ∧ q) 6 ¬p ∨ ¬q 43 52 Lógica y Cálculo Proposicional Tautologías y Contradicciones 44




Tabla De Verdad Expresiones Logicas Logica



Nanopdf Com Download Apuntes Logica Proposicional Pdf
Crear una tabla de verdad con ceros y unos con proposionesHttp//cursosgratis316blogspotcom/Evalua el esquema (p ∨ q) → (∼ p ∧ q) , tabla de verdad logica proposicional , ejercicio resuelto Construir las tablas de verdad para 1 (p ∧ q )→ (p V q) 2 (p V q) ↔ ¬(q V ¬q) 3 (p v ¬q) V (¬ q ∧ ¬ q) Recibe ahora mismo las respuestas que necesitas!




Calameo Tablas De Verdad



Tabla De Verdad De La Bicondicional
Analice el valor de verdad de (P ⇒ Q) ∧ (P ∧ ¬ Q) sabiendo que P es v y Q es f 8 Represente simbólicamente en la Lógica de proposiciones la proposición El producto de los números reales a y b es distinto de 0 si y solo si a y b son diferentes de 0 Solución ab ≠ 0 ↔ a ≠ 0 y b ≠ 0View Tablas de Verdad3ppt from ECONOMIC MISC at University of Guanajuato TABLAS DE VERDAD (pΔq)↔r∧q∧(p←s) Es verdadero o falso?Una vez que hayas introducido el enunciado, elige el tipo de tabla que quieres (Verdadero/Falso) o (1/0), y haz clic en Generar y automáticamente se creará la tabla de verdad, si la quieres guardar puedes clicar en para descargarla como png




Logica Matematica




Calameo Tablas De Verdad
3 EJERCICIO 607 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfa cibles ¬(p → q) p ∨ q p q ¬(p → q) p ∨ q V V F V V F V V F V F V F F F F Las dos fbfs son simultáneamente satisfacibles, ya que son V a la vez en la 2ª interpre tación EJERCICIO 608 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfaCapítulo I Lógica proposicional 3 13 Operadores lógicos Negación Dada una proposición p su contraria no p es verdadera cuando aquella es falsa y se simboliza ¬p p ¬p 0 1 1 0 Conjunción o producto lógico Dadas dos proposiciones p, q, el producto lógico es la proposición molecular p y q que se simboliza (p ∧ q) p q p ∧ q 0 0 0OPERACIONES LÓGICAS Y TABLAS DE VERDAD La validez de una proposición compuesta depende de los valores de verdad de las proposiciones simples que la componen y se determina mediante una tabla de verdad 1 Conjunción Vincula dos proposiciones mediante el conectivo lógico "y" Tabla de Verdad F F F F V F V F F V V V p q p ∧ q




Tautologia Contradiccion Contingencia Ejercicios Resueltos De Implicacion Y Equivalencia Logica Pdf



Lgica Proposicional Conceptos Bsicos Proposiciones Atmicas O Elementales
2 respuestas Valero Angel Serrano Mercadal Respondido el 12 de julio de 21 El autor tiene 1,5 K respuestas y 281,5 K visitas a sus respuestas Es decir, de esta manera (p ∧Observe la tabla de verdad de ¬p ∧ q Nótese que las tablas de verdad de ¬p ∨ q y p→q son idénticas; Luego selecciona la alternativa correcta (p → q)↔ r≡0 (p v r ) ∧ (q→p) ¬ (p ∧ r)↔ (q v r) i=0;




Necesito Ayuda Con La Siguiente Tabla De Verdad Pq Pvq V Qv P Brainly Lat



1
TABLAS DE VERDAD Estas tablas pueden construirse haciendo una interpretación de los signos lógicos, ¬ , ∧ , ∨ , → , ↔ ,como no, o, y, sientonces, sí y sólo si, respectivamente La interpretación corresponde al sentido que estas operaciones tienen dentro del razonamiento1 Determinar la validez de los siguientes razonamientos, mediante tablas de verdad (p → q) ∧(r → ¬q) ⇒ (r → ¬p) (p → ¬q) ∧ (¬r → ¬q) ⇒ (p → ¬r) 2 Demostrar la validez de los siguientes razonamientos, mediante reglas de inferencia p∨q ¬p→q ¬p∨¬q s→(p∧¬p)Iii=0 Determine los valores de verdad de a, b y c, para que la siguiente proposición sea falsa




Resolver Tabla De Verdad P Q P R R P Brainly Lat




Logica Y Calculo Proposicional 2
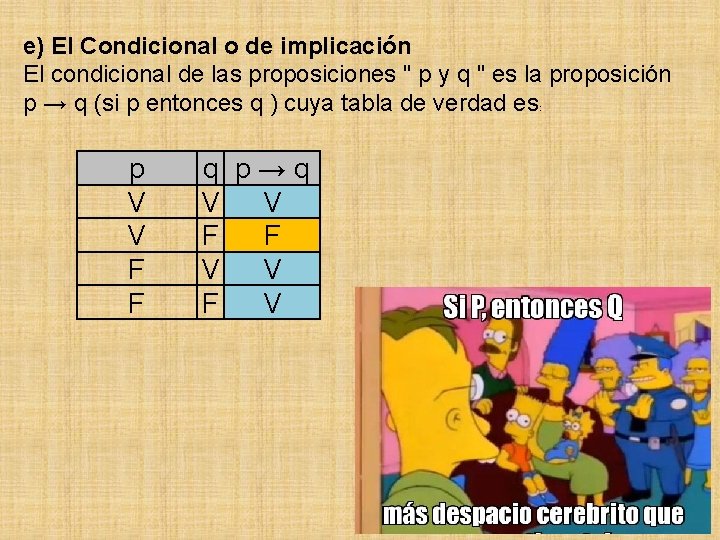
• p solamente si q (o solamente si q entonces p de la tabla de verdad de p → q, sabemos que si p → q es verdadera y p también es verdadera, entonces q debe ser verdadera, por tanto, siendo p verdadera, es suficiente para que también q lo sea Ésto es, p es suficiente para q tiene el mismo significado que p → q16 Se sabe que la proposición (p v q) ∧ p ⇒ (r v q) ⇔ p es falsa Determinar los valores veritativos de las proposiciones a) p, q, r b) (p ∧ ∼ q) ⇒ (r v p) ⇔ ∼ q (r v p) 17 Construir las tablas de verdad de y verificar cuales de ellas son tautologías a) (p ∧ ∼q) ⇒ q ⇔ (p ⇒ q)Respectivamente, halla el valor de verdad de las siguientes proposiciones a) p ∧ r b) q ∨ ∼ q c) q ∧ (r ∨ p) d) r ∧ ∼ (p ∨ q)




Logica1 Ejercicios Resueltos6 Interpretacion Filosofia Verdad Logica




Confeccion Tablas De Verdad 14
Símbolo (~) Este operador lógico operador binario que requiere que las niega o cambia el valor de verdad de dos proposiciones sobre las que actúa una proposición o sentencia sean verdaderas para producir un valor verdadero Todos los demás casos dan p ~p como resultado un valor falso F V p q p∧q V F F F FSuponga que¬pes una proposici ́on verdadera Si sabe que la proposici ́on (p⇔ (q∨r))⇒ (s∧r) es falsa, determine el valor de verdad de la proposici'on (q∧s)∨r Determine si la siguiente proposici ́on {p∧ (p⇒q)}es l ́ogicamente equivalente conp Utilice algebra proposicional para mostrar las siguientes equivalencias de" LÓGICA I " EJERCICIOS RESUELTOS – 6 TEMA 6 – SEMÁNTICA TABLAS DE VERDAD Y RESOLUCIÓN VERITATIVOFUNCIONAL




Erick Vizcaino Actividad Paso 2 Solucion A Ejercicios




Logica1 Ejercicios Resueltos6 Lgica I Ejercicios Resueltos 6 Tema 6 Semntica Tablas De Verdad Y Resolucin Veritativo Funcional Ejercicio 6 01 Course Hero
En la tabla de verdad vas a tener 7 proposiciones distintas r, p, q, r o p, no q, (r o p) y no q, y por último, si (r o p) y no q entonces p Lo único que tienes que hacer es ir verificando cada proposición conforme a las 8 combinaciones de r, p y q;(p ∧ q) → r 4 Tablas de valores de verdad * Evaluar un esquema molecular es obtener la matriz principal * El número de valores que se asigna a cada variable es «2n», donde «n» es el número de variables * Es importante jerarquizar los esquemas antes de evaluarlosEs decir, ambas son falsas sólo en el segundo caso Por consiguiente, p→q es lógicamente equivalente a ¬p ∨ q;




Proposiciones Conjunciones Disyunciones Implicaciones Eric Pacheco Blog




Logica Tablas De Verdad Veracidad
3) Mediante una tabla de verdad comprueba las siguientes equivalencias lógicas a) p ↔ q ≡ (p ∧ q) ∨ (∼ p ∧ ∼ q) b) ∼ (p ∨ q) ≡ ∼ p ∧ ∼ q c) p → q ≡ ∼ p ∨ q 4) Si los valores veritativos de "p", "q" y "r" son V, F y V;Implicaciones de sus componentes p ↔ q ⇔ (p → q) ∧ (q → p) La tabla de verdad, donde puede verse que esta regla se cumple, o sea, que ambas proposiciones son equivalentes, es la siguiente p q p ↔ q p → q q → p (p → q) ∧ (q → p) Realizar las siguientes tablas de verdad 1 q Δ p 2 q ∧ p 3 (p ∨ q) ↔ r 4 (p → q ) ∨ q No Respondan cualquier estupidez por favor



1




Tablas De Verdad Y Logica Proposicional Articulo De La Maquina Oraculo
Pero (p −→ q) ∧ q es verdad sólo si p −→ q es verdad y q también lo es, luego una de las lı́neas de su tabla de verdad serı́a p q p −→ q (p −→ q) ∧ q (p −→ q) ∧ q −→ p F V V V F Por tanto, (p −→ q) ∧ q −→ p no es una tautologı́a y el argumento no serı́a válido, es decir, es una falaciaEs decir, p→q ≡ ¬p ∨ q PROBLEMAS Y EJERCICIOS 1 Sean p "Hace frío" y q "Está lloviendo"Si "s" y "s ~ (p v q)" son verdaderas, indique los valores de verdad a) ~ (p ~q) b) (p q) v ~s c) s v (q p) 7 Si V (p) = V, q y r dos proposiciones cualquiera Halla el valor de a) ~ q (~p v ~q) b) (r v ~p) (q v p) r c) q (p q) (q ~p) 08 Construye la tabla para a) p → (q ∧ r) b) (p → ¬ r) ↔ (q v r) 09




1 Encuentro Ejercicios De Logica
.gif)



Logica Proposicional Ejercicios Resueltos De Nivel Preuniversitario Pdf
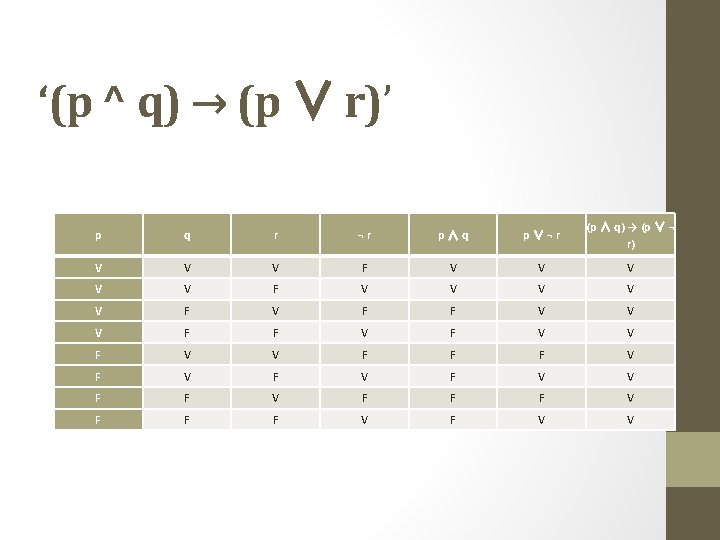
9927 construcciones s a, inspeccionará los sistemas eléctricos y las instalaciones mecánicas en una planta del sector industrial la detección temprana y confiable de daños en componentes de sistemas relevantes a la producción es esencial para poder garantizar la seguridad y confiabilidad del sistema esto implica que es posible la reducción de costosos tiempos de9) (p ∧q)∨(p∨q) 10 ) (p ∧(¬q))∧p 11 ) ((p∨q)∧(¬r))∧r Actividad 6 Construye una tabla de verdad para cada una de las siguientes proposiciones compuestas, donde p, q y r, denotan proposiciones primitivas verdad de la proposición (α→((¬p∨q)∧(¬r) ))∧¿Cómo sería el tableau o la tabla de verdad de esta proposición (~p—>q) v r ^ ~s v q — r?



Unidad 3 La Logica




Logica Matematica Discrete Mathematics Pagina 2




Logica Matematica



Q Tbn And9gctrgp9fgvfhmyshths2lefjjggzpjhlhycvpt8rc Uygzsy0n Usqp Cau




Principales Leyes Logicas Y El Metodo Abreviado Ciencias Basicas




Pdf Tablas De Verdad Jorge Sangurima Academia Edu




Definicion De Una Tabla De Verdad Ciencias Basicas



Nanopdf Com Download Ejercicios De Simplificacion De Seccion 7101 13 Pdf



Ejercicios De Logica Tablas De Verdad Docsity




Logica Matematica 13 Ii Capitulo 2 Tautologia




Generador De Tablas De Verdad Logica Proposicional Algebra Booleana




Tautologia Contradiccion Y Contingencia




Construye La Tabla De Verdad De La Siguiente Proposicion P Q P Q Brainly Lat



Un Ejemplo De Articulacion De La Logica Y La Geometria Dinamica En Un Curso De Geometria Plana




Tablas De Verdad Logica Proposicional Matematica Youtube



6 Costruccuon De Tablas De Verdad Recursos Didacticos



Tablas De Verdad Una Tabla De Verdad O



Nanopdf Com Download Ejercicios De Simplificacion De Seccion 7101 13 Pdf




Alguien Sabe Como Hacer Estos Ejercicios De Tablas De Verdad 1 P Q R2 P Q P Q Brainly Lat




Solucion Actividad 1 Logica Matematica Expresiones Logicas




Capitulo I Logica Y Conjuntos Ppt Descargar




Tabla De Verdad Tautologia Youtube




Calameo Ejercicios Tablas De Verdad




Tablas De Verdad




Doc Formalizacion Y Valoracion De Proposiciones Cristhian Bacusoy Academia Edu



Solucionado Matematicas Discretas Lo Que S Mal




Logica Matematica




Determina La Tabla De Verdad De Pvq P Brainly Lat




P Q P R Q R Es La Negacion De P Q Tabla De Verdad Brainly Lat




P Q Q R R S P S R R Realizar Tabla De Verdad Brainly Lat




1 1 Logica Proposicional




Contradiccion Wikipedia La Enciclopedia Libre




Taller Logica Conjuntos 2




Ejercicios Resueltos Sobre Tabla De Verdad Docsity




Contradiccion Wikipedia La Enciclopedia Libre




Tablas De Verdad Ejercicio 1 Youtube




Tabla De Verdad Wikipedia La Enciclopedia Libre




Propositional Logic Tautologias Indeterminaciones Y Contradicciones




Paso 2 Proposiciones Y Tablas De Verdad Trabajos




Tablas De Verdad Como Completar Una Tabla De Verdad Con Las Proposiciones Dadas Youtube




Logica Matematica



Generador De Tablas De Verdad Logica Proposicional Algebra Booleana




Introduccion Al Pensamiento Matematico Actividad 4 Proposicion Semantica




Mat 115 Practica De Construccion De Tabla De La Verdad




Generador De Tablas De Verdad Logica Proposicional Algebra Booleana




Tablas De Verdad Logica Proposicional Matematica Youtube




Tablas De Verdad Algebra Ppt Descargar




Tablas De Verdad Ejercicio 1 Youtube




Anexo 1 Tarea Proposicion Logica Matematica




Logica Y Calculo Proposicional 2




Calameo Ejemplo Vimeo




Erick Vizcaino Actividad Paso 2 Solucion A Ejercicios




Calameo Practico Logica



Tablas De Verdad Una Tabla De Verdad O Tabla De Valores De Verdad Es Una Tabla Que Muestra El Valor De Verdad De Una Proposicion Compuesta Para Cada Ppt Descargar




Ejercicios Resueltos De Tablas De Verdad




Tablas De Verdad Negacion Y Conjuncion Youtube




Logica Proposicional




Instituto Tecnologico De Pachuca Logica Proposicional Ppt Descargar




Semana1 5 Pdf Proposicion Si Y Solo Si




Generador De Tablas De Verdad Logica Proposicional Algebra Booleana




Calameo Ejercicios De Tablas De Verdad




Ejercicios De Logica Tablas De Verdad Docsity




Sin Usar Tablas De Verdad Demuestre Que La Siguiente Proposicion Es Una Tautologia Brainly Lat




Calameo Ejercicios De Tablas De Verdad




Logica General By Unmsm Prolex Issuu




Tabla De La Verdad




Construir Las Tablas De Verdad Para 1 P Q P V Q 2 P V Q Q V Q 3 P V Q V Brainly Lat



1




Logica Proposicional Ppt Descargar




Tabla De Verdad 1 Pdf Contradiccion Proposicion




Tablas De Verdad Una Tabla De Verdad O Tabla De Valores De Verdad Es Una Tabla Que Muestra El Valor De Verdad De Una Proposicion Compuesta Para Cada Ppt Descargar




Ejercicios De Simplificacion De Ecuaciones Logicas 1 Studocu




01 Logica Proposicional



Http Www Uca Edu Sv Matematica Upload W File Matem C3 A1tica 1 ing guia sobre l C3 93gica Pdf




Tablas De Verdad Y Formalizacion De Argumentos Apunt En Taringa




Logica Matematica


